If, like me, you've been exposed to a lot of fun math games, you've probably played Sprouts before. If not, don't worry, as it's a simple game, and I'll explain how to play in just a few paragraphs. In any case, I've always been taught that it's a purely tactical game–in other words, that there aren't grand and overarching strategies that guide your every move, just quick tactics you can use to get an edge in the moment.* But I decided to investigate Sprouts myself, and to my surprise, there's an effective and relatively simple winning strategy that you can use to defeat anyone who doesn't know the strategy!**
But I decided to investigate Sprouts myself, and to my surprise, there's an effective and relatively simple winning strategy that you can use to defeat anyone who doesn't know the strategy!
What is that strategy? You'll have to read the entire post to find out, mwahaha!***
Introduction
Happy Tuesday, my loyal followers, and welcome back to Chromatic Conflux! And to my disloyal followers, loyal nonfollowers, and disloyal nonfollowers, happy Tuesday as well. I strongly encourage you to become a loyal follower. In any case, I'll start by describing the rules of Sprouts. I will then introduce the notion of lives, and segue into how you can use that to gain an advantage at the game.
The Rules
For a different and perhaps spicier explanation of Sprouts then the one I will provide you with, I suggest watching this Vsauce2 video on the topic from about 1:52 to 3:30. (Or watch the entire video–the title is clickbait, but it's not boring, and it sets the stage nicely for this post.) If you watched the video, or already understand Sprouts, you can skip to the next section, Lives.
Anyway, here's how to play Sprouts. Start by drawing some dots. Three dots should make for a game that's quick but not too quick–but you can play with any number of dots.
On your turn, connect two dots with a line. The line can be straight or curved–in fact, it's even legal to connect a dot to itself. However, lines can't cross other lines.
Then, add a new dot to the line. It can be anywhere on the line, but it doesn't matter where you put it.
Then it's your opponent's turn!
One more constraint, though. Dots can never have more than three lines coming out of them. Therefore, if a dot already has three lines through it, it's a dead dot, and nothing can connect to it anymore.**** Normally, I like to cross out dead dots to make it clear that you can't do anything with them. However, sketch.io, the website I'm using to make these pictures, has a broken heart tool, so I'll use that instead.
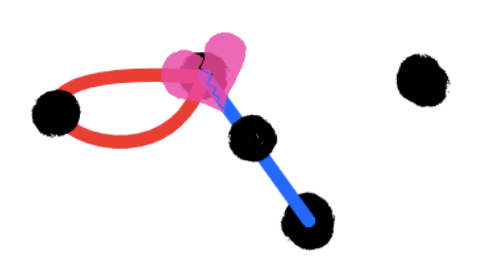
Rinse, repeat. If you can't make a line, you lose. In other words, the last player to move wins.
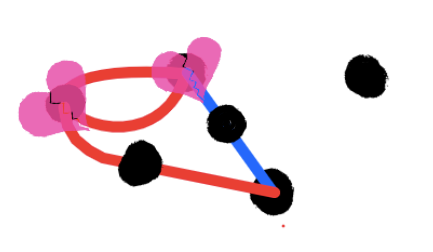
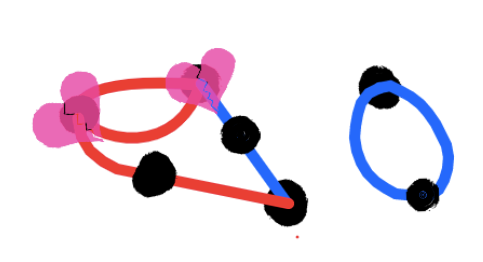
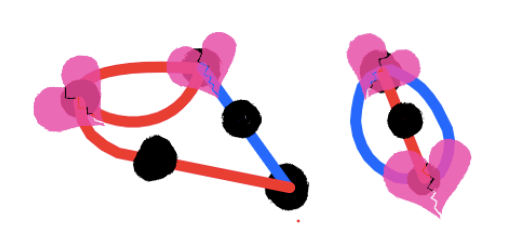
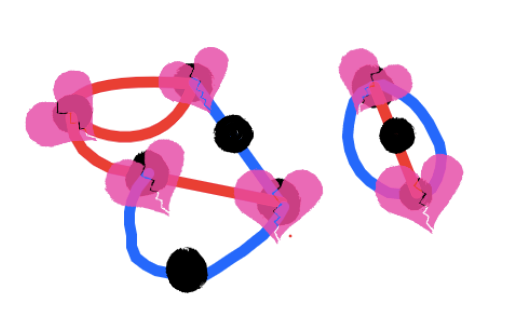
In this game, you won as red, since blue can't make a move. The only dots that are still alive can't be connected without going through another line.
Lives
Every dot has three lives to begin with, because you can draw three lines touching it before it dies. You might assume that a dot with one line connected to it would, therefore, have two lives. That said, you know what happens when you assume–it's something you do every second, and these assumptions are calibrated to be correct the vast majority of the time.***** In this case, you'd be right.
That said, you know what happens when you assume–it's something you do every second, and these assumptions are calibrated to be right the vast majority of the time.
Similarly, when you have multiple dots (most of the time–we'll get to the exception later on), you simply add up the number of lives each dot has. Let's do an example–how many lives does this position, from the above game, have?
Well, the top right dot has no lines coming out of it. So it provides 3 lives. The bottom dot has only one line coming out of it, adding 2 lives. The one above it has lines on its top and its bottom, but still has room for one more. 1 life. Similar situation with the top left, so 1 more life. The top middle dead dot, with its heart broken, doesn't provide a single life. That's a total of 7 lives in this position.
Every Move Subtracts A Life
What happens to the number of lives a position has when you make a move? Well, both ends of the line connect to a dot, and that removes 2 lives total. However, when you draw a line, you also add a new dot to the line. This new dot already has two lines through it–both ends of the one you drew–so it adds 1 life to the position. If you subtract 2 lives and add 1, that's the same as subtracting 1. So every move made subtracts 1 life from the position.
So every move made subtracts 1 life from the position.
Interlude: The Caterpillar in the Well
Before we get back to Sprouts, I'm going to talk about a different mathematical puzzle that will help us understand the game a bit better. (I'm not sure where I originally heard this puzzle, but I found a variant on this website after an Internet search.) Anyway, the problem.
A caterpillar is at the bottom of a 30-inch well and wants to climb up and out of the well. Every day, the caterpillar is able to climb 3 inches, but every night, while the creature is sleeping, it slips 2 inches. How many days does it take for the caterpillar to escape from the well? You might reason that since the caterpillar nets 1 inch per day, it would take 30 days to climb out. However, on the 28th day, the caterpillar climbs from 27 inches up to the top of the well. It doesn't slide back down that night, because it's out of the well! So the answer is 28 days.
I Lost the Game
In a three-dot game, after how many moves must the game end? Well, three dots have 9 lives, and each move subtracts 1 life–so we would be tempted to say 9. But recall the caterpillar in the well. Each move doesn't really subtract 1 life; each move subtracts 2 lives and adds 1. So if a position has 1 life, there are no moves remaining, because we can't subtract 2! This makes sense–if the only living dot has two lines coming out of it, there's no dot to connect it to, even if we will theoretically regain that life when we put a new dot on the line.
This gives us an easy way to find the maximum number of moves possible in a game of Sprouts: triple the number of dots and subtract 1. For a three-dot game, this gives us 8 moves possible.
This gives us an easy way to find the maximum number of moves possible in a game of Sprouts: triple the number of dots and subtract 1.
Additionally, this tells us that there is no strategy in Sprouts, since every move subtracts the same 1 life. In a three-dot game, there are 8 moves, right? This suggests that Player 2 will be the last to move, and therefore, they will always win.
But wait a second. In the sample game I showed you earlier in the post, you'll note that red won. But red was Player 1!
Gonna Make This Garden Grow
Count the number of lives in the ending position. You'll see that there are 2, each each living dot has two lines connected to it. But those two dots are incapable of connecting to each other.
In fact, this position has two of what I call gardens. A garden is a clump of dots and lines such that only 1 life remains when no player can move. You can clearly see the two gardens in the final position–there's the left garden, with most of the dots and lines, the right garden, which has only two lines and three dots.
In any case, each garden has 1 life remaining, and recognizing this is the key to winning at Sprouts. With a three-dot or 9-life game, player 2 wins the one-garden game, whereas player 1 wins the two-garden game. (Player 2 wins the three-garden game, and so on, though this is impossible without cooperation between the players.) So the first player's essential goal is to divide the board into two gardens, whereas the second player is attempting to prevent this.
General Strategy
Now you have all the background you need, so here's the general strategy:
When the game begins with an odd number of dots, Player 1 wants an even number of gardens, and Player 2 wants an odd number of gardens.
When the game begins with an even number of dots, Player 1 wants an odd number of gardens, and Player 2 wants an even number of gardens.
You can simply remember the fact that Player 2 always wants the dots and gardens to have the same parity, and Player 1 always wants them to have opposite parity. Here's a bad mnemonic so you won't forget this: One and Opposite both start with O.
Here's a bad mnemonic so you won't forget this: One and Opposite both start with O.
Opening Strategy
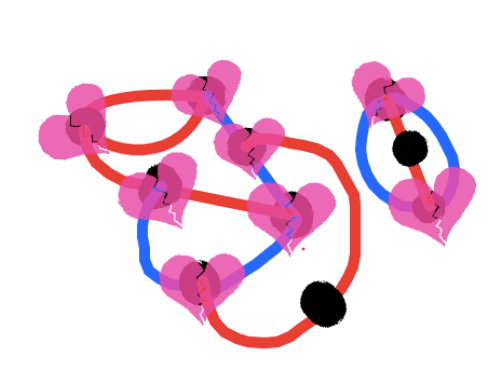
I've already hit my normal word length, but I can't resist going into one specific opening strategy. If you're Player 1 in the three-dot game, there is an opening that guarantees you a win. Draw a line connecting one dot to itself, encircling exactly one other dot, like in the picture below.
By building a wall estranging the top middle dot from the bottom right dot, this ensures two gardens, giving you the win no matter what else happens in the game. Technically, Player 2 can try to make three gardens, but you can easily block this.
Conclusion
And that's the strategy. What did we learn along the way? That not everything that's worth figuring out has already been figured out. Explore.
Also, inch by inch, row by row, make this garden grow, but only if you're Player 1 in the odd-dot game or Player 2 in the even-dot game. Remember the strategy, people.
–beautifulthorns
*There's no luck in Sprouts. Therefore, if you're a computer, you can analyze all possible outcomes and use that to determine your move. It's legitimate to think of this as a winning strategy, but if you don't have a cheat sheet or photographic memory, it's not one that you can learn, so I won't consider this it a strategy for the purposes of this blog post.
**By the way, I considered titling this post "Professor Sprouts" or something like that, but I couldn't think of a way to phrase it that felt clever.
***Or just scroll down to the bottom, but that's basically cheating.
****You might wonder why it's considered to have three lines coming out of it if only two lines have been drawn this entire game. Well, the red line connects to it twice, so it counts as two lines for the purposes of that dot.
In other news, if a dot has two lines coming out of it, you can't connect it to itself. This doesn't come up much, but I figured I'd mention it in this footnote anyway.
*****Ironically, in this bait-and-switch you may have incorrectly assumed that I would go for the other joke. Here's an xkcd on the subject for bonus points.